Elo Scoring

Two players have Elo scores $A$ and $B$.

With no info other than that, it’s generally accepted that

$P(A\ beats\ B) = 1 / (1 + 10^{(B - A) / 400})$

If A indeed does beat B, here are the new Elo scores:

• $A’ = A + K \cdot (1 - P(A\ beats\ B))$

• $B’ = B - K \cdot (1 - P(A\ beats\ B))$

Where $K$ is a hyperparameter, usually something between 10 and 40.

If A and B go to a draw, this is the update rule:

• $A’ = A + K \cdot (0.5 - P(A\ beats\ B))$

• $B’ = B - K \cdot (0.5 - P(A\ beats\ B))$

So $A$ and $B$ are pulled towards one another.

Chess.com gives new players an Elo of 400 to start.

Statistical Intuition

The first time I saw this, I thought it was gobbledygook. Then I made this graph:

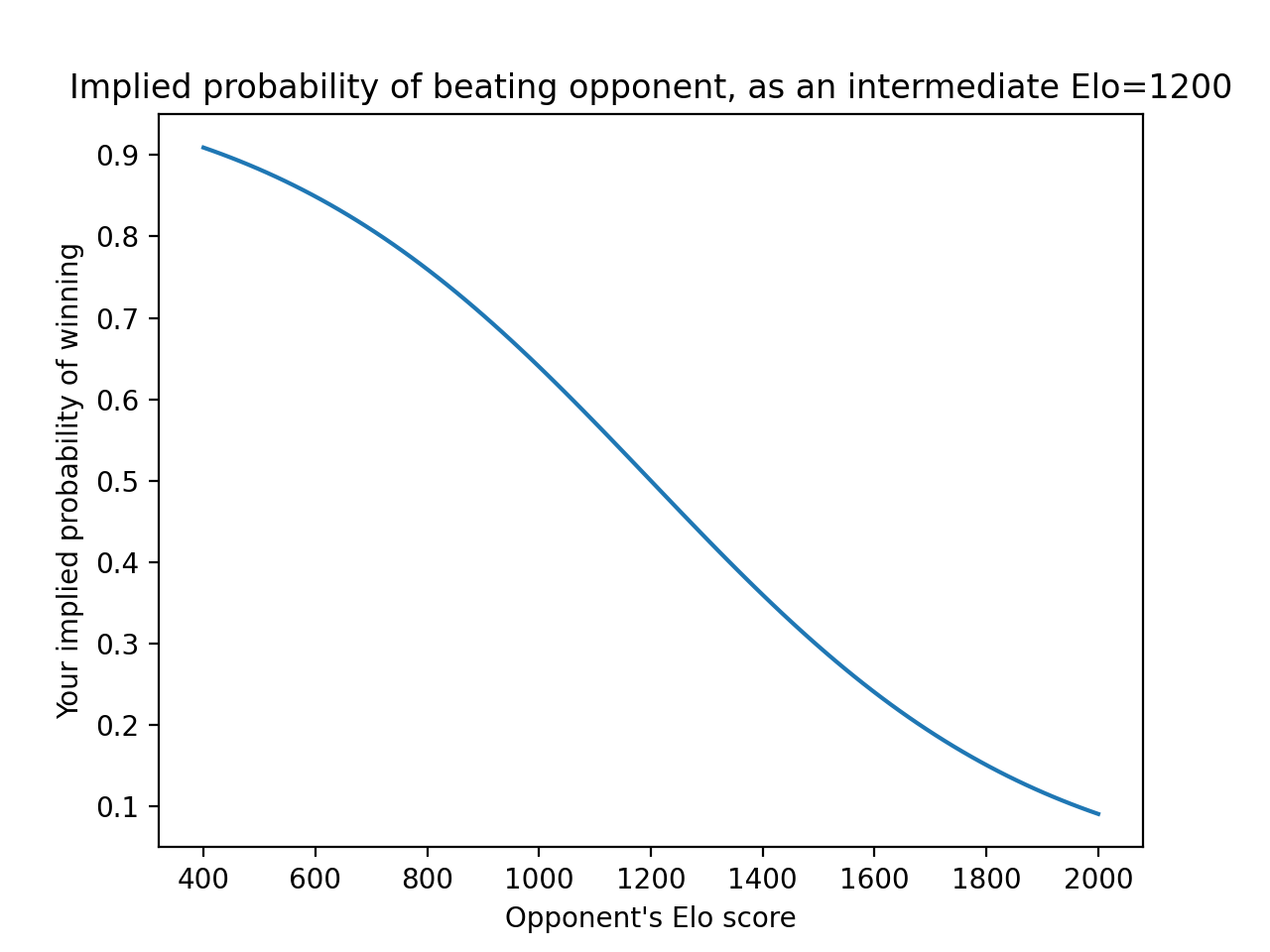
Turns out, with some algebraic manipulations, one can show that the following is an equivalent system:

• Let $X_A$ be a one-hot encoding of the chess player $A$
• Let $Y$ be $1$ if A beat B, $0.5$ if they draw, and $0$ if B beat A

$P(A\ beats\ B) = 1 / (1 + e^{-\beta^T (X_A - X_B)})$

That looks familiar, right? It’s logistic regression without an intercept term. To show these are equivalent, set $A = \frac{400}{\ln 10} \beta^T X_A$.

And then, for the update rule:

$ \beta’ = \beta + \alpha (Y - P(A\ beats\ B))^T (X_A - X_B)$

Ignoring draws, this is the gradient of the binary cross-entropy loss, with the learning rate $\alpha$ equivalent to a scaled K-factor.

So the Elo rating system is stochastic gradient descent on a really, really wide logistic regression model, with a batch size of 1. Every player gets a coefficient, which is their Elo score.

Is this really more intuitive?

Criticisms of the Elo rating system cost a dime a dozen. For instance, suppose you compete in a tournament, and you lose your first match against a similarly-ranked opponent. For your own ego’s sake, you should hope that guy does well in the rest of the tournament - if he also beats everyone else, you can believe that his original Elo was an underestimate.

I believe Elo scores in chess culture play a role similar to that of Black-Scholes in finance. Nobody treats the model as gospel anymore, yet it laid the foundation for options trading as a large, legitimate industry with many participants. Its primary utility is as a shorthand, a social convention, a lingua franca; anything more sophisticated would be a worse coordinating mechanism.

For a large number of people to adopt a system, and to mutually employ its outputs to interact with each other, it must be as simple as possible. Had the logistic regression model not been burned into my brain, I would find it far less intuitive than the original Elo formulation, and at any rate impossible to calculate.

It adds a new dimension to my understanding of the otherwise almost trite saying: all models are wrong, but some are useful.